It's been a long time since I last looked at electronics equations and whilst I can sort of remember what they are about, I'm finding that it's not nearly as fresh as it used to be, so maybe a small but of revision is needed? Well it is for me so... back to basics.
Kirchoff's Circuit Laws
These two laws are almost so obvious as that they seem not worth mentioning, that is, when you already know them.
The first is
Kitchoff's Current Law, this says that at any node on a circuit the total current leaving the circuit must equal the total current entering it.
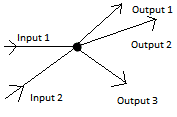 |
| KCL |
In the diagram above, the sum of all the inputs equals the sum of all the outputs... No matter how many there are!
The second law, is
Kirchoff's Voltage Law . This law states that the potential difference around any loop (closed circuit) must be zero.
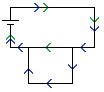 |
| KVL | |
So, in the diagram above, the battery is causing a potential difference of some volts; Let's say that the battery is supplying 9V, this means that the total of all the voltage drops (or raises, if there was another battery) around either possible loop must be -9V.
Ohms Law
Ohm realised that the current around a circuit was proportional to the potential difference applied to it. In other words, if you doubled the voltage, then you doubles the current. He called the coefficient the resistance and gave the equation:
V = I / R
Where V is the voltage, I is the current and R is the resistance.
In the circuit above, the resistors have values of 1,000 ohms and 2,000 ohms.
 |
| Circuit with resistors |
|
In order to work out the voltage over each resister we need to work out what the current in this circuit is.
To do that, we need to know how to sum up multiple resistances. Resisters in series and simple summed by adding their values together, but in parallel equation is:
1/RTotal = Sum(1/Rn)
This means that the total for the circuit is 1666.66 ohms. Which means that the total current leaving the battery must be I = V/R = 9/1666.66 = 0.0054 Amps.
How is this split when we get to the junction?
I like to work this out by looking at the ration of the resistance. However, there are two ways and sometimes one is easier than the other.
Firstly, the ratio of the resistors is 1:2 so, 1 third of the current will go through R3 and 2 thirds will go through R2, i.e. 0.0018 Amps through R2 and 0.0036 Amps through R1. Simple!
Now, the other method.
We need to work out the potential drop across R1 (the voltage drop). We can use Ohms Law for this, the current is 0.0054 Amps, and the resistance is 1,000 Ohms so the drop is 5.4 volts. This means that the drop over R2 & R3 is 9V - 5.4V which is 3.6 volts.
Now, just use Ohms Law again to work out the current through each one.
Current through R2 = 3.6 / 2000 = 0.0018 Amps
Current through R3 = 3.6 / 1000 = 0.0036 Amps
Same result as we got before.
Maybe this isn't allot of help to anyone who's been playing with electronics for a while, but writing it out has helped me refresh this stuff...
Power
Power, in physics, is a measurement of the speed at which something can do work. Work, in physics, is the amount of energy something has expended in performing a task and it is measured in Watts.
In an electric circuit, the formular for power is this:
P = IV
Now, look at this basic circuit:
The current in this circuit is I = V / R = 9 / 1000 = 0.009 Amps. Therefore the power P = 9 * 0.009 = 0.081 Watts
If we substitute Ohm's Law we can see that:
P = IV = I (I * R) = V (V /R)
Next, capacitance!









